www.drpt.net/brainfarm.it

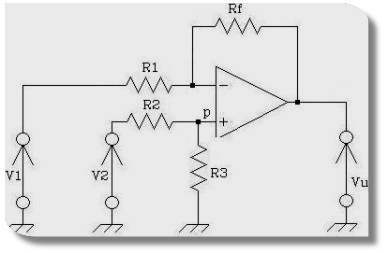
Questo tipo di amplificatore è chiamato così perché consente di avere in uscita un segnale uguale alla differenza dei due segnali applicati in ingresso.


Studio del funzionamento:
Anche il differenziale è un sistema lineare. Applicheremo, per il suo studio il principio della sovrapposizione degli effetti.

I° Passo:
Mettendo il generatore V1 in corto avremo la resistenza R1 direttamente collegata a massa. Otterremo così una configurazione non invertente simile a quella del sommatore non invertente, secondo la quale:

Vu’ =(1+Rf /R1)*Vp

Vp è la tensione che si genera sulla resistenza R3, che forma un partitore di tensione con la resistenza R2 e il generatore V2. Vp sarà quindi:

Vp =R3 *V2 /(R2 +R3)

Sostituendola nella formula di prima si ottiene:

Vu’ =[(1+Rf /R1)]*[R3 /(R2 +R3)]*V2

II Passo:

Mettendo il generatore V2 in corto avremo la resistenza R2 direttamente collegata a massa. Sulle resistenze R2 ed R3, non può circolare corrente in quanto, la corrente che arriva dal generatore V1 è 0 (zero) a causa della resistenza d’ingresso dell’amplificatore che è infinita. Non potendosi creare nessuna differenza di potenziale sulle due resistenze R1 ed R2, esse non causano nessun effetto. Otterremo così una configurazione invertente, secondo la quale:

Vu’’ = -V1 *Rf /R1

III Passo:
Sommando gli effetti avremo che:

Vu =Vu’ +Vu’’

e cioè:

Vu =[(1+Rf /R1)]*[R3 /(R2 +R3)]*V2 -(V1 *Rf /R1)

Anche qui, se costruissimo il circuito con tutte le resistenze uguali tra di loro, la formula del differenziale diventerebbe:

Vu =V2 -V1

Guardando questa formula, si nota che il segnale in uscita è la differenza dei due segnali applicati in entrata.

Tabella riassuntiva delle caratteristiche del circuito:
· Resistenza d’ingresso: per V= R;per V= R+R
· Amplificazione: Vu=[(1+Rf/R)]*[R/(R+R)]*V(V*Rf/R)
· Amplificazione con tutte le resist. uguali: Vu=VV
· Resistenza d’uscita: teoricamente nulla.

Home

Articolo

Pagina articolo:
<< -